【科技前沿】第13期：广义特征值极小扰动问题研究进展

【编者按】为了更好地营造校园学术氛围，传播我校学术科研动态，即日起，学校在校园网开辟“科技前沿”专栏，定期总结、回顾学校师生取得的科研成果。欢迎广大师生及时把自己的学术科研成果以邮件的形式告诉我们，我们希望获得您以下成果信息：为政府、企业、媒体进行了专业咨询；科技成果通过了相关鉴定；科技成果落地、实现产业化；发表了高水平的学术论文；获得了专利授权；出版、编著了专著、教材；获得了科技奖励；在重要学术会议上进行了发言……

我们愿意为有学术追求的师生搭建一个交流的平台，希望在师生的努力下，学校的学术氛围可以日益浓厚，让我们为实现电子信息特色鲜明的国内高水平大学而奋斗。联系邮箱：dwxcb@guet.edu.cn。

近日，我校数学与计算科学学院李姣芬教授、段雪峰教授与华南师范大学黎稳教授、美国Southern Illinois UniversityMingQingXiao教授在数值计算国际权威学术期刊《Advances in Computational Mathematics》和《Journal of Scientific Computing》分别在线发表了题为“Newton’s method for the parameterized generalized eigenvalue problem with nonsquare matrix pencils”和“A Riemannian Optimization Approach for Solving theGeneralized Eigenvalue Problem for Nonsquare MatrixPencils的学术论文。《Advances in Computational Mathematics》和《Journal of Scientific Computing》是Springer出版社旗下数学学科数值计算方向老牌期刊，分布创刊于1993年和1986年，现均为中科院2区和JCRQ1,2021年影响因子分别为1.990和2.592。

求解广义特征值问题是当今科学与工程计算界的热点之一，其在有限元分析、结构振动、线性系统理论等领域有广泛应用。对于非方复矩阵对广义特征值的具体计算一般存在两个难点：a)可能不存广义特征值；b)对扰动很敏感。2005年国际数值代数权威专家GENE H. GOLUB和新加坡国立大学DELIN CHU等人引入广义特征值极小扰动模型，并从代数层面将原问题转化为紧集约束下的一类矩阵优化问题，并指出针对求解此类矩阵优化问题设计有效算法有待解决。

该两篇论文另辟蹊径，从黎曼优化角度分析问题并设计求解算法。首先基于复矩阵和实矩阵的同构映射将问题进一步转化为乘积流形下的黎曼优化问题，结合乘积流形几何性质，提出了黎曼非线性共轭梯度和预处理黎曼牛顿求解算法。针对形式复杂的黎曼牛顿方程，基于复矩阵拉直算子和Kronecker乘积，将其转化容易求解的标准实对称线性方程组。 丰富的数值实验和数值比较验证了所提算法较已有的基于交替最小二乘和总体最小二乘的算法在迭代速度和解精度上的优势。该研究成果得到了University of Oxford国际知名数值代专家Yuji Nakatsukasa（arXiv:2109.05384, 2021）和国内同行（arXiv:2110.08774， 2021、arXiv:2110.08754, 2021，Numerical Linear Algebra with Applications，2021）等的正面引用。

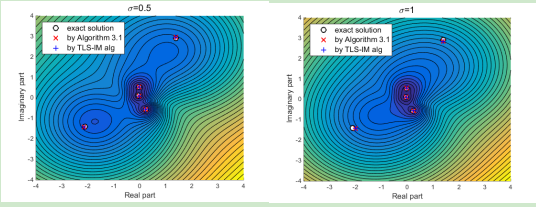
图一、不同扰动下复矩阵对广义特征值在复平面的分布图

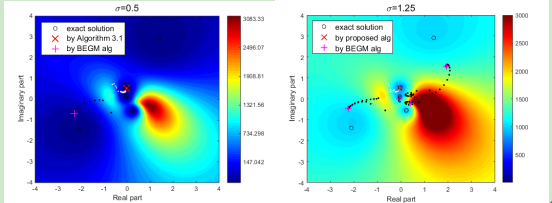
图二、不同算法迭代点所对应的广义特征值在复平面的运动轨迹

该研究工作同时得到了国家自然科学基金、广西自然科学杰出青年基金和广西自然科学基金面上项目的资助。